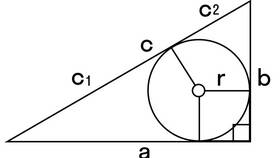
В прямоугольном треугольнике сумма двух острых углов всегда составляет 90 градусов. Это фундаментальное свойство вытекает из теоремы о сумме углов треугольника и особенностей прямоугольных фигур.
Содержание
Доказательство свойства
- Рассмотрим прямоугольный треугольник ABC с прямым углом C (∠C = 90°)
- По теореме о сумме углов треугольника: ∠A + ∠B + ∠C = 180°
- Подставим значение прямого угла: ∠A + ∠B + 90° = 180°
- Перенесем 90° в правую часть: ∠A + ∠B = 180° - 90°
- Получаем: ∠A + ∠B = 90°
Геометрическая интерпретация
| Угол | Обозначение | Свойство |
| Первый острый | ∠A | Меньше 90° |
| Второй острый | ∠B | Меньше 90° |
| Прямой | ∠C | Ровно 90° |
Практические следствия
- Если известен один острый угол, второй вычисляется как 90° минус первый
- Два острых угла прямоугольного треугольника всегда дополняют друг друга до прямого угла
- В равнобедренном прямоугольном треугольнике оба острых угла равны по 45°
Примеры расчетов
Пример 1: Нахождение неизвестного угла
Дан прямоугольный треугольник с одним острым углом 30°. Тогда второй острый угол равен: 90° - 30° = 60°
Пример 2: Проверка треугольника на прямоугольность
Если в треугольнике сумма двух углов составляет 90°, третий угол обязательно будет прямым (180° - 90° = 90°)
Применение в геометрических задачах
- Решение задач на подобие треугольников
- Вычисление тригонометрических функций
- Доказательство равенства треугольников
- Построение геометрических фигур
Историческая справка
Это свойство было известно еще древнегреческим математикам и активно использовалось Евклидом в его "Началах". Оно лежит в основе многих геометрических построений и тригонометрических расчетов.
Заключение
Свойство суммы острых углов прямоугольного треугольника является важным инструментом в геометрии. Его понимание позволяет решать широкий класс задач и служит основой для более сложных математических концепций. Запомните простое правило: в прямоугольном треугольнике два острых угла в сумме всегда дают прямой угол.